Scale and Conformal Invariance, Limit Cycles

The Renormalization Group (RG) is an important tool in theoretical physics. It can be used to understand a physical system on different scales, that is, when looked at under magnifying glasses with different magnification. Well, I really don't mean “magnifying glass” literally. The physical system may be studied in atom smashers, like the LHC at CERN, or with coherent light sources, like the one at SLAC. But the point is that these can probe many different scales of a physical system.

In a nut-shell, the RG tells us that a system described by some dimensionless parameters when observed at some scale is in fact described by the same number of parameters but with different numerical values at some other scale.

Mathematically we study the RG through an equation (RGE). It is a differential equation, meaning that it gives the rate at which one must change the parameters as the scale of observing is varied.

My colleagues and I quite accidentally stumbled upon a surprise, when studying the RGE. We found “limit cycles.” These is what the picture shows.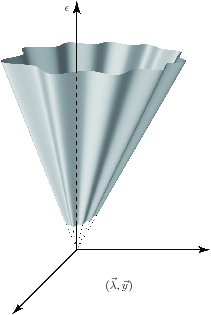 The parameters of the theory are indicated as lambda and y on the horizontal plane of the figure, while the vertical axis, labeled by epsilon, gives different theories. For fixed epsilon you get a slice that looks like a wiggly, closed contour, representing a solution of the RGE in which the parameters lambda and y are changing as the scale is changing, eventually coming to the starting point but now at a very different scale. This is weird, but we eventually proved that the the physics is exactly the same anywhere on the limit cycle.

We are now studying the connection to other questions, including the possibility of proving an a-theorem in 4- and 6-dimensional quantum field theory.