The Renormalization Group (RG) is an important tool in theoretical physics. It can be used to understand a physical system on different scales, that is, when looked at under magnifying glasses with different magnification. Well, I really don't mean “magnifying glass” literally. The physical system may be studied in atom smashers, like the LHC at CERN, or with coherent light sources, like the one at SLAC. But the point is that these can probe many different scales of a physical system.
In a nut-shell, the RG tells us that a system described by some dimensionless parameters when observed at some scale is in fact described by the same number of parameters but with different numerical values at some other scale.
Mathematically we study the RG through an equation (RGE). It is a differential equation, meaning that it gives the rate at which one must change the parameters as the scale of observing is varied.
My colleagues and I quite accidentally stumbled upon a surprise, when studying the RGE. We found “limit cycles.” These is what the picture shows.
The parameters of the theory are indicated as lambda and y on the horizontal plane of the figure, while the vertical axis, labeled by epsilon, gives different theories. For fixed epsilon you get a slice that looks like a wiggly, closed contour, representing a solution of the RGE in which the parameters lambda and y are changing as the scale is changing, eventually coming to the starting point but now at a very different scale. This is weird, but we eventually proved that the the physics is exactly the same anywhere on the limit cycle.
We are now studying the connection to other questions, including the possibility of proving an a-theorem in 4- and 6-dimensional quantum field theory.
In the “Standard Model” we have a very successful mathematical model of the known particles of matter and of the strong, weak and electromagnetic forces that act on them. Take a look at the Review of Particle Physics. You will find page upon page of tabulations of properties of elementary particles and their reactions, many measured with remarkable precision. And all of it is explained by the Standard Model!
But the thing is, absent a Higgs field the Standard model says the fundamental particles, like quarks and leptons, as well as the mediators of the weak interactions, are massless. But they ain't. And if there is a Higgs field, there must be a higgs particle: just like quantum fluctuations of, say, the electromagnetic field manifest themselves as particles we call photons, so do quantum fluctuations of the higgs field manifest themselves as particles, “higgs bosons.” Sure, there are alternative theories explaining the masses of fundamental particles that don't contain a particle like the higgs boson, but (1) they are ugly compared to the Standard Model, and, most importantly, (2) the higgs boson has been seen! Check out the higgs-observation pages of the ATLAS and CMS experiments at CERN.
My higgs-boson-related research has addressed several questions. The first one is clear: how do we know what we have seen is the higgs boson? If it walks like a duck and quacks like a duck, … may it be a scaup or a smew? It turns out that there is a large class of models that contain no higgs field, but they all predict the existence of a particle called a “dilaton” and, my collaborators and I showed, in first approximation the dilaton behaves just like a higgs! This begs the next question, how do you tell them apart? Or more generally, how do you know it is the higgs of the Standard Model? The answer is that you make very careful measurements and compare with theoretical predictions. For example, my students and I made some computations showing that the very rare 3-body decays of the higgs can be sensitive probes of deviations from the Standard Model.
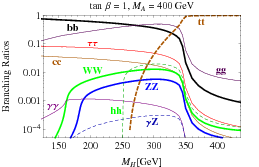
The picture you clicked on, reproduced here, is from a paper with my student Patipan, in which we looked at a simple but popular extension of the Standard Model in which there are two higgs fields. This turns out to mean there are two neutral higgs particles, a charged higgs particle (plus its oppositely charged anti-particle) and a third neutral particle, a kind of cousin of the higgs. Hypothesis: one of the two neutral higgs particles corresponds to the particle observed at CERN. Question, from the measured properties of that particle, what can you say about the others. The figure has one of the answers. It gives, as a function of the unknown mass of the second neutral higgs, what fraction of the time that second higgs decays into different combinations of particles. With other students we later extended the study to include whole classes of extensions of the Standard Model and found theoretical upper bounds on the masses of the hypothetical particles (good news for LHC experiments that, after all, are limited in the range of masses of particles they can produce). (Note: it is fundamental constituents (like quarks and leptons) of the elementary particles (like baryons and mesons) that are mass.
My page on the Higgs-boson tells you about the Standard Model (SM), but mostly in the context of the higgs boson and asking the question how do we know what we have seen is the higgs boson. Well, let's be more open-minded, in spite of all it successes, how do we know the Standard Model is correct?
There are theoretical arguments pointing to the incompleteness of the SM, like the “hierarchy problem” and the “strong CP problem”, which however do not technically require modifying the model. More relevant are observations pointing to the incompleteness of the SM. We know, for example, that the universe is filled with transparent matter, inaptly called “dark-matter,” which however cannot be made of normal stuff, where by “normal stuff” I mean matter made of the particles described by the SM. The SM is certainly incomplete, but not necessarily incorrect. The dark-matter could well be stuff that interacts with normal stuff only gravitationally, so that it does not really require modification of the SM.
But once in a while there is an anomaly, an experiment design to check yet another aspect of the SM that does not give the SM-expected result. One such case is the anomalously large top-quark Forward-Backward asymmetry observed by two experiments, CDF and D0, at Fermilab. If you want to know what this ominous sounding “top-quark Forward-Backward asymmetry” is, and how can it arise, here is my awesome attempt at an explanation for non-experts.
The figure is from a paper with colleagues Kagan and Zupan from Cincinnati and Trott from
CERN, and shows that in explaining the observed Fermilab data the new physics (“NP”)
contribution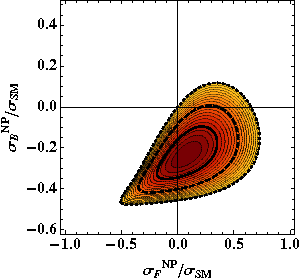 
to the cross section in the backward direction has to be negative while its
contribution in the forward direction has to vanish, or at best be slightly positive. A contribution
to a cross section can be negative if the interference between the NP and SM contributions
is negative. But how can that be truein the backwards dierection and not in the forward
direction? That puts a tough constraint on which can of NP can explain this. We went on to
explore models that were predicated on Minimal Flavor Violation, a scheme that automatically
avoided, or largely avoided, additional tough constraints on the new models from such
esoteric things as the rate of neutral kaon and Beauty meson mixing (see also here).
Incidentally, the explanation on Forward-Backward asymmetry was prepared in connection with a paper with my student, Chris Murphy, in which we studied the asymmetry but now for bottom -quarks rather than top-quarks. Bottom quarks are called beauty quarks in Europe, they always have had different taste than americans! Chris realized that beauty quarks would be sensitive probes of theNP that had been proposed to explain the observed the anomaly in the top quark FB-asymmetry. This is specially the case since the bottom quark is so much lighter than the top quark that resonant production of bottom-quark pairs occurs for energies comparable to the rest energy of the Z-particle (one of the mediators of the weak interactions). When this happens, the interference between the Z and other production mechanisms results in large amplification of the other mechanisms, including those hypothesized in NP models. We are still waiting for the experimental result!!
In the “Standard Model” (SM) we have a very successful mathematical model of the known particles of matter and of the strong, weak and electromagnetic forces that act on them. Take a look at the Review of Particle Physics. You will find page upon page of tabulations of properties of elementary particles and their reactions, many measured with remarkable precision. And all of it is explained by the Standard Model!
The SM has 18 adjustable parameters. This is quite excellent for a model that predicts a myriad reactions, often with spectacular precision, including dependence on all sorts of kinematic variables, for example, angular and energy dependence of the outcome of collisions between elementary particles. So you could say, wow, all those predictions with only 18 adjustable parameters. But we particle theorists are quite ambitious, so we'd like to reduce the number. Most of the parameters of the SM have to do with the masses of the quarks and leptons and with the quark mixing angles (these measure how they share in the weak interactions). The branch of particle physics that deals with phenomena associated with transitions between types of quarks is called “Flavor physics” --- because we call “flavors” the different types of quarks. So if you know the proton is made of two “up” (or “u”) quarks and one “down “ (or “d”) quark, you should know that “u” and “d” are two different “flavors.” The complete list of flavors in ascending order according to their mass is up, down, strange, charm, bottom (or beauty, in Europe) and top (or truth in Europe, although this has fallen out of use of late).
Much of the 90s I spent developing tools for producing precise predictions of the SM that involve flavor physics and could be tested experimentally. Moreover, the techniques allowed for precise determination of some of the 18 fundamental parameters. I was motivated by strong experimental programs dedicated to this type of physics, BaBar in SLAC and Belle in KEK (Japan). See my old page.
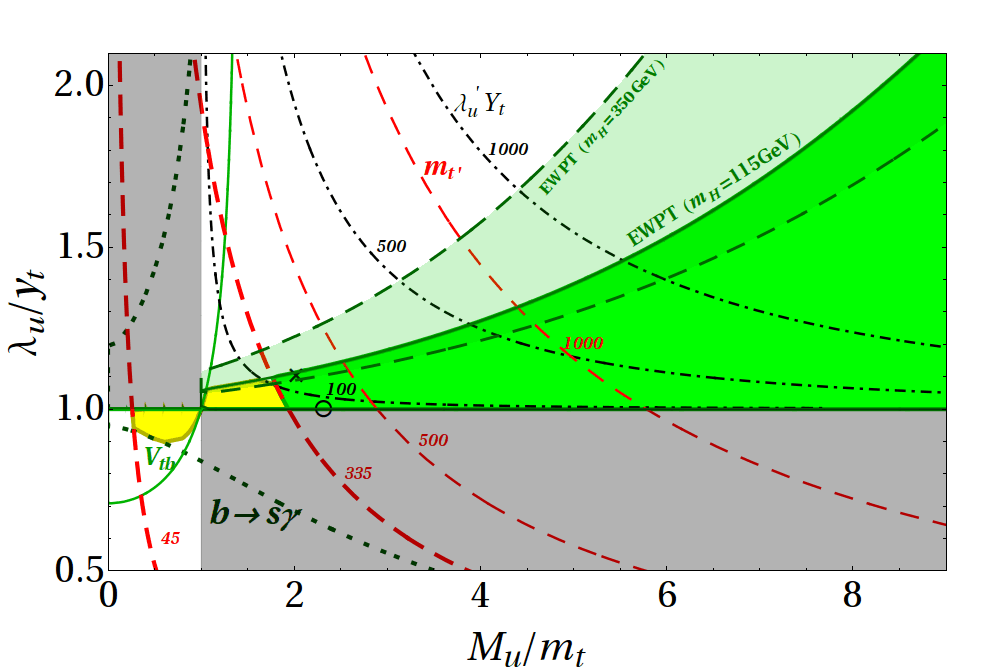
But now that we have established that the SM is pretty good at explaining all of these flavor transitions, and have extracted the parameters with excellent precision (well, most of them), I have turned my attention to other questions. The figure shows the result of a study with then CERN postdocs Redi and Villadoro of a model we invented, in the same publication, that attempts to explain the flavor parameters of the SM through dynamics. We are not the first to do this, but our model is very different from others, so it is worth exploring. The figure shows, as a function of two parameters of the model, the region that is definitely not ruled out experimentally (in green), the region that may or may not be ruled out, depending of additional details (in yellow) and contours of fixed mass of a new particle, the t' (in red).
Email me at bgrinstein@ucsd.edu
University of California, San Diego
Department of Physics, Mail Code-0319
9500 Gilman Dr. #0319 La Jolla, CA 92093-0319 USA
